Notes on Real-time Quadratic Conic Programming

Homogeneous Self-dual Embedding(HSDE) IPM, Homogeneous Embedding(HE) IPM, HE Douglas-Rachford Splitting(DRS)

I. Introduction

Whether in the filed of general STEM subjects, or control and GNC, modeling and solving of optimization problem are increasingly being based as the fundamental paradigm, from upper-layer problem and its numerical algorithm. Especially after IPM theory became mature in 1990s and computing performance of microcontroller chips have been enhanced in 2010s, designs and algorithms based on convex optimization have been introduced into control and GNC, such as [robust control with LMI, OCP trajectory generation with IPM, parameter identification with LS]{.underline}, and so on. These advancements have simultaneously spurred breakthroughs in applied engineer theories and products across multiple industrial fields, including but not limited to [soft landing rockets, robots, ADS, unmanned aircrafts and many autonomous systems]{.underline}, also neural network, protein design and other large-scale optimization.

During 30 years, various optimization algorithms and corresponding numerical packages have emerged, and evolves according to different problems’ feature and size. For convex(conic) problems, there are three dimensions for solvers' classification,

1.{Primal, Primal-dual},

From local optimal condition KKT, primal-dual based algorithms are mainstream in the accuracy, convergence and robustness, like Augmented Lagrangian Method(ALM), IPM, and so on.

2.{First-Order, Second-Order}

IPM, as a typical second-order method, utilizes second-order derivative information (Hessian Matrix) of objective and constraints, to update newton iterative direction, while ADMM, as a typical first-order method, only has $o(1/k)$ convergence speed.

3.{IPM, Exterior Point Method(Penalty)}

All central path of IPM is located in convex cones (inequality constraints), while penalty function method replaces hard constraints with soft cost, so iteration points might violate inequality constraints.

In control and GNC on embedded system, real-time, low computational load, hard constraints, robustness are the desired features. Therefore, only the three types of solvers and corresponding softwares are focused, for real-time trajectory generation's OCP on embedded system:

i. Homogeneous Self-dual Embedding(HSDE) IPM for Linear SOCP : ECOS

ii. Homogeneous Embedding(HE) IPM for Quadratic SOCP: Clarabel

iii. HE Douglas-Rachford Splitting(DRS) for Quadratic SOCP: SCS
and a similar variant, Proportional-integral projected gradient method (PIPG)

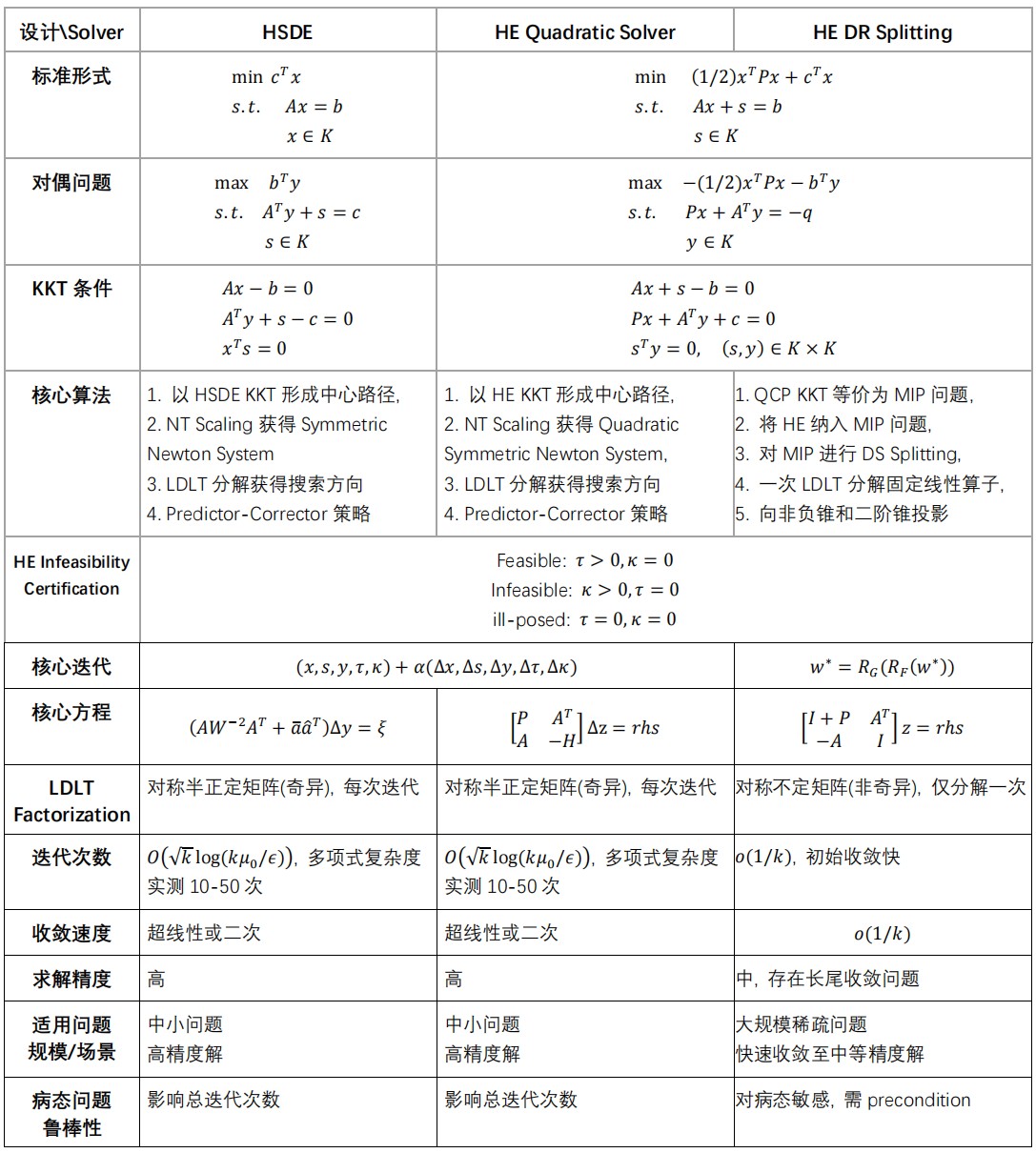
The main designs and performance are listed in tables.

Generally among three solvers, HE DRS is preferred for real-time platform, due to the advantages:

  • Infeasibility Certification concurrent with convergence, by Homogeneous Embedding;

  • Converges rapidly to local modest precision solution, by first-order splitting iteration;

  • Low computational load of single iteration, by conical projection and fixed LDLT decomposition,
    compared to updated decomposition of each iteration in IPM's newton direction;

  • Warm-start, beneficial for MPC.

solver_comparision

II. Primal-dual IPM for Linear Conic Problem

LSOCP问题的KKT条件为

\[{Ax - b = 0}\ {A^{T}y + s - c = 0}\ {x^{T}s = 0}\]

Self-dual Model统一了从初始不可行解向可行解和最优值的收敛过程，

\[\min{\ \ \ \ \ \beta v}\] \[{s.t.\ \ \ \ \ \ Ax - b\tau - r_{p}v = 0 }{\ \ \ \ \ \ \ \ \ \ \ - A^{T}y + c\tau - s - r_{d}v = 0 }{\ \ \ \ \ \ \ \ \ \ \ {- c}^{T}x + b^{T}y - \kappa - r_{g}v = 0 }{\ \ \ \ \ \ \ \ \ \ \ r_{p}^{T}y + r_{d}^{T}x + r_{g}\tau = - \beta }{(x,s,\tau,\kappa) \in K \times K \times R_{+} \times R_{+},\ (y,v)\ is\ free}\]

对扰动的KKT系统使用Newton迭代求解，代入变量组的一阶近似$(x + \Delta x,s + \Delta s,y + \Delta y,\tau + \Delta\tau,\kappa + \Delta\kappa)$以获得Newton迭代方向$(\Delta x,\Delta s,\Delta y,\Delta\tau,\Delta\kappa)$

\[A\Delta x - b\Delta\tau = r_{p}v - (Ax - b\tau)\] \[- A^{T}\Delta y + c\Delta\tau - \Delta s = r_{d}v - \left( - A^{T}y + c\tau - s \right)\] \[{- c^{T}\Delta x + b}^{T}\Delta y - \Delta\kappa = r_{g}v - \left( {- c}^{T}x + b^{T}y - \kappa \right)\] \[X(\Delta S)e + S(\Delta X)e = v\mu_{0}e - XSe - \Delta X\Delta Se\]

\(\kappa\Delta\tau + \tau\Delta\kappa = vu_{0} - \tau\kappa - \Delta\tau\Delta\kappa\) where $\ \Delta X = mat(T\Delta x),\ \Delta S = mat(T\Delta s)$

Mehrotra Predictor-Corrector Strategy将KKT Newton方向的求解分为两步，Predictor进行激进优化，而Corrector校正方向靠近中心路径。

最终获得HSDE IPM for Linear SOCP的算法流程如下，

+—————————————————————————————————————-+ | HSDE IPM for Linear SOCP | +================================================================================================================+ | Input: Accuracy parameter$\mathbf{\epsilon > 0}$, | | $\left( x_{0},s_{0},y_{0},\ \tau_{0},\kappa_{0} \right) \in K \times K \times R^{m} \times R_{+} \times R_{+}$ | | | | Output: $(x,s,y,\tau,\kappa),\ g,\ flag.{ pfeas,dfeas,opt}$ | +—————————————————————————————————————-+ | 1. function HSDESolver$\left( A,\ b,c,K,x_{0},s_{0},y_{0},\ \tau_{0},\kappa_{0} \right)$ | | | | 2. $(x,s,y,\tau,\kappa)\mathbf{=}\left( x_{0},s_{0},y_{0},\ \tau_{0},\kappa_{0} \right)$ | | | | 3. while ${g = x}^{T}s + \tau\kappa > \epsilon$ do | | | | 4. calculate Scaling $W,W^{- 1}$, construct $AW^{- 2}A^{T}$, | | | | 5. $LDL^{T} = AW^{- 2}A^{T}$, get Calculation Flow at first time | | | | 6. Predictor: solve KKT with $v = 0,E_{xs} = 0,\ E_{\tau\kappa} = 0$, get | | $\left( \Delta x_{p},\Delta s_{p},\Delta y_{p},\Delta\tau_{p},\Delta\kappa_{p} \right)$ | | | | 7. calculate step $\alpha_{p}$ | | | | 8. update centering parameter $v$, and $E_{xs},\ E_{\tau\kappa}$ | | | | 9. Corrector: solve KKT with $v,E_{xs},\ E_{\tau\kappa}$, get | | $(\Delta x,\Delta s,\Delta y,\Delta\tau,\Delta\kappa)$ | | | | 10. calculate step $\alpha$ | | | | 11. calculate next iteration point: | | $(x,s,y,\tau,\kappa) + \alpha(\Delta x,\Delta s,\Delta y,\Delta\tau,\Delta\kappa)$ | | | | 12. end while | | | | 13. switch | | | | 14. case 0: $\tau > 0,\ \kappa = 0,and\ g > \epsilon$, $(x,s,y) = \lbrack x,s,y\rbrack./\tau$, | | flag.feas=true, flag.opt=false; | | | | 15. case 1: $\tau > 0,\ \kappa = 0,and\ g < \epsilon$, $(x,s,y) = \lbrack x,s,y\rbrack./\tau$, | | flag.feas=true, flag.opt=true; | | | | 16. case 2: $\kappa > 0,\ \tau = 0,\ and\ b^{T}y > 0$, flag.pfeas=false; | | | | 17. case 3: $\kappa > 0,\tau = 0,\ and\ c^{T}x < 0$, flag.dfeas=false; | | | | 18. case 4: $\tau = 0,\ \kappa = 0$ flag.feas=false; | | | | 19. end switch | | | | 20. return $(x,s,y,\tau,\kappa),\ g,\ flag.{ pfeas,dfeas,opt}$ | | | | 21. end function | +—————————————————————————————————————-+ | | +—————————————————————————————————————-+

III. Operator Splitting For Quadratic Conic Problem

尽管Primal-dual IPM可以实现高精度、二次收敛和多项式复杂度的求解，但迭代过程需重复对KKT线性系统进行LDLT分解，单次迭代的成本较高，且对热启动(Warm-Start)的支持较差。因此对大规模锥优化问题，或实时嵌入式OCP问题，单次迭代成本较低、快速收敛至中等精度、支持热启动的Primal-dual一阶方法更优。基于ADMM或Douglas-Rachford Splitting(DRS)的算子分裂法(Operator Splitting)的求解器被开发并广泛使用，如QSQP, SCS, COMSO等。

3.1 LCP Form of QSOCP’s KKT Conditions

二次目标锥优化问题的KKT互补松弛条件为，
\(Ax + s - b = 0,\ \ \ Px + A^{T}y + c = 0,\ \ \ s^{T}y = 0,\ \ \ \ \ (s,y) \in K \times K^{*}\) 可被重写为线性互补问题(Linear Complementarity Problem, LCP)，

\({s\bot y\ \ \ \Leftrightarrow \ \ \ {s^{T}y = x}^{T}Px + c^{T}x + b^{T}y = 0 }{R^{n} \times K \ni \begin{bmatrix} x \\ y \end{bmatrix}\bot\begin{bmatrix} 0 \\ s \end{bmatrix} = \begin{bmatrix} Px + A^{T}y + c \\ b - Ax \end{bmatrix} \in \left\{ 0 \right\}^{n} \times K\ }\)定义为LCP($M,q,C$)问题的形式为

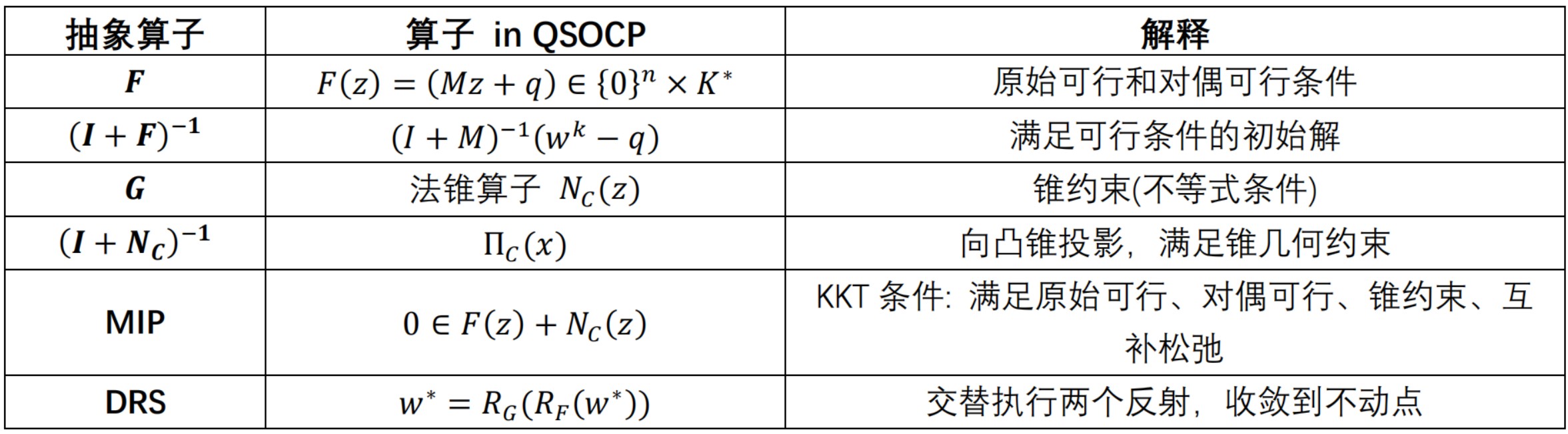
\[R^{n} \times K \ni z\bot F(z) = (Mz + q) \in \left\{ 0 \right\}^{n} \times K^{*}\] \[z = \begin{bmatrix} x \\ y \end{bmatrix},\ M = \begin{bmatrix} P & A^{T} \\ - A & 0 \end{bmatrix},\ q = \begin{bmatrix} c \\ b \end{bmatrix}\]

3.2 DRS for QSOCP

综上，对QSOCP的原始KKT条件()应用DRS分解。首先推导算子$\ F\ $的预解操作，

\({w \in (I + F)\widetilde{u} = \widetilde{u} + F\left( \widetilde{u} \right) = \widetilde{u} + M\widetilde{u} + q }{\widetilde{u} = (I + M)^{- 1}(w - q) }\)其次为法锥算子的预解操作，

\(u^{k + 1} = \left( I + N_{C} \right)^{- 1}\left( 2{\widetilde{u}}^{k + 1} - w^{k} \right) = \Pi_{C}\left( 2{\widetilde{u}}^{k + 1} - w^{k} \right)\) 即保持变量$\ x \in R^{n}\ $不变，变量$\ y\ $中的等式约束变量不变，向非负锥和二次锥投影。

因此，DRS迭代过程如下

\[^{k + 1} = (I + M)^{- 1}\left( w^{k} - q \right) }{u^{k + 1} = \Pi_{C}\left( 2{\widetilde{u}}^{k + 1} - w^{k} \right)}\]

\(w^{k + 1} = w^{k} + u^{k + 1} - {\widetilde{u}}^{k + 1}\) 可直观理解DRS中的操作，

抽象算子 算子 in QSOCP 解释 ——————————————————————————- ————————————————————- —————————————— \(\mathbf{F}\) \(F(z) = (Mz + q) \in \left\{ 0 \right\}^{n} \times K^{*}\) 原始可行和对偶可行条件

\(\left( \mathbf{I}\mathbf{+}\mathbf{F} \right)^{\mathbf{- 1}}\) \((I + M)^{- 1}\left( w^{k} - q \right)\) 满足可行条件的初始解

\(\mathbf{G}\) 法锥算子 $N_{C}(z)$ 锥约束(不等式条件)

\(\left( \mathbf{I}\mathbf{+}\mathbf{N}_{\mathbf{C}} \right)^{\mathbf{- 1}}\) \(\Pi_{C}(x)\) 向凸锥投影，满足锥几何约束

MIP \(0 \in F(z) + N_{C}(z)\) KKT条件: 满足原始可行、对偶可行、锥约束、互补松弛

DRS \(w^{*} = R_{G}(R_{F}\left( w^{*} \right))\) 交替执行两个反射，收敛到不动点 —————————————————————————————————————————————————————————————-

4.2 数值计算

4.2.1 锥投影

定义一个点$\ v\ $到一个凸集$\ K\ $的投影为，

\[\Pi_{K}(v) = \arg{\min_{x \in K}\left| |x - v| \right|^{2}}\]

由于法锥算子的预解操作等价为向锥投影，因此非负锥和二次锥的投影具有解析解。

1.A 非负锥投影
非负锥定义为${\ K}{\leq 0},\ { x \in R{n} x \geq 0}$，则整个向量$\ v\ $到非负锥$\ R_{+}^{n}\ $的投影$\ \Pi_{R_{+}^{n}}(v)\ $就是每个分量取正部，
\[\Pi_{R_{+}^{n}}\left( v_{i} \right) = \max\left( 0,v_{i} \right)\]
1.B 二阶锥投影
SOC定义为$\ K_{2} = \ \left{ (t,x) \in {R \times R}_{n} \right \ x {2} \leq t}$，给定点$\ v = (t,x)\ $向$\ K{2}\ $的投影需分情况讨论，

1) 若$v\ $在锥内部，则其投影就是自身

\[\Pi_{K_{2}}(v) = v\]
2) 若$v\ $在”反向锥”内部，$ x _{2} \leq - t\ $，即t为负数，则其投影为原点
\[\Pi_{K_{2}}(v) = (0,0)\]

3) 其他情况均投影到${\ K}_{2}\ $的边界上，其解析解为

\[\Pi_{K_{2}}(v) = \frac{|x| + t}{2|x|}\begin{pmatrix} |x| \\ x \end{pmatrix}\]

投影点是该点与圆锥轴线构成的二维平面内，向圆锥边界（一条射线）所做的垂足。

4.2 $\mathbf{F\ }$预解算子的稀疏分解

代入KKT条件的矩阵，原始$\ \mathbf{F}\ $预解算子的方程为

$${(I + M){\widetilde{u}}^{k + 1} = rhs,\ \ \ rhs = \left( w^{k} - q \right) }{\begin{bmatrix} I + P & A^{T} \

  • A & I \end{bmatrix}\begin{bmatrix} \widetilde{x}
    \widetilde{y} \end{bmatrix} = \begin{bmatrix} \mu_{x}
    \mu_{y} \end{bmatrix} }$$可见$\ (I + M)\ $并非对称矩阵，因此将第二行取反
\[\begin{bmatrix} I + P & A^{T} \\ A & - I \end{bmatrix}\begin{bmatrix} \widetilde{x} \\ \widetilde{y} \end{bmatrix} = \begin{bmatrix} \mu_{x} \\ {- \mu}_{y} \end{bmatrix}\]

则可获得$\ R\ $为对称不定矩阵(非奇异)。因为优化问题$\ A\ $的数值在迭代过程中不变，因此仅需要在初始进行稀疏LDLT分解，后续迭代过程仅需要代入不同右值的方程，仅乘法求解即可，所以DRS每次迭代的计算复杂度低。即便OCP SCP过程的子问题的变量或参数发生变化，但$\ A\ $和$\ P\ $的稀疏模式(Sparse Pattern)相同，也可离线生成固定问题的定制化求解器。

V. Reference {#v.-reference .标题3z}

[1] Domahidi, A., Chu, E., & Boyd, S. (2013, July). ECOS: An SOCP solver for embedded systems. In 2013 European control conference (ECC) (pp. 3071-3076). IEEE.
[2] Goulart, P. J., & Chen, Y. (2024). Clarabel: An interior-point solver for conic programs with quadratic objectives. arXiv preprint arXiv:2405.12762.
[3] O'Donoghue, B. (2021). Operator splitting for a homogeneous embedding of the linear complementarity problem. SIAM Journal on Optimization, 31(3), 1999-2023.